Glossary of ring theory

Ring theory is the branch of mathematics in which rings are studied: that is, structures supporting both an addition and a multiplication operation. This is a glossary of some terms of the subject.

1 Definition of a ring
2 Types of elements
3 Homomorphisms and ideals
4 Types of rings
5 Ring constructions
- 5.1 Polynomial rings
6 Miscellaneous
7 Ringlike structures
8 See also
9 Notes
10 References

Definition of a ring

Ring: A ring is a set R with two binary operations, usually called addition (+) and multiplication (*), such that R is an abelian group under addition, a monoid under multiplication, and such that multiplication is both left and right distributive over addition. Note that rings are assumed to have multiplicative identities unless otherwise noted. The additive identity is denoted by 0 and the multiplicative identity by 1.

Subring: A subset S of the ring (R,+,*) which remains a ring when + and * are restricted to S and contains the multiplicative identity 1 of R is called a subring of R.

Types of elements

Central: An element r of a ring R is central if xr = rx for all x in R. The set of all central elements forms a subring of R, known as the center of R.

Divisor: In an integral domain R, an element a is called a divisor of the element b (and we say a divides b) if there exists an element x in R with ax = b.

Idempotent: An element r of a ring is idempotent if r² = r.

Unit or invertible element: An element r of the ring R is a unit if there exists an element r⁻¹ such that rr⁻¹=r⁻¹r=1. This element r⁻¹ is uniquely determined by r and is called the multiplicative inverse of r. The set of units forms a group under multiplication.

Irreducible: An element x of an integral domain is irreducible if it is not a unit and for any elements a and b such that x=ab, either a or b is a unit. Note that every prime element is irreducible, but not necessarily vice versa.

Prime element: An element x of an integral domain is a prime element if it is not zero and not a unit and whenever x divides a product ab, x divides a or x divides b.

Nilpotent: An element r of R is nilpotent if there exists a positive integer n such that rⁿ = 0.

Zero divisor: A nonzero element r of R is a zero divisor if there exists a nonzero element s in R such that sr=0 or rs=0.

Homomorphisms and ideals

Factor ring or quotient ring: Given a ring R and an ideal I of R, the factor ring is the ring formed by the set R/I of cosets {a+I : a∈R} together with the operations (a+I)+(b+I)=(a+b)+I and (a+I)(b+I)=ab+I. The relationship between ideals, homomorphisms, and factor rings is summed up in the fundamental theorem on homomorphisms.

Finitely generated ideal: A left ideal I is finitely generated if there exist finitely many elements a₁,...,a_n such that I = Ra₁ + ... + Ra_n. A right ideal I is finitely generated if there exist finitely many elements a₁,...,a_n such that I = a₁R + ... + a_nR. A two-sided ideal I is finitely generated if there exist finitely many elements a₁,...,a_n such that I = Ra₁R + ... + Ra_nR.

Ideal: A left ideal I of R is a subgroup of R such that aI ⊆ I for all a∈R. A right ideal is a subgroup of R such that Ia⊆I for all a∈R. An ideal (sometimes called a two-sided ideal for emphasis) is a subgroup which is both a left ideal and a right ideal.

Jacobson radical: The intersection of all maximal left ideals in a ring forms a two-sided ideal, the Jacobson radical of the ring.

Kernel of a ring homomorphism: The kernel of a ring homomorphism f : R → S is the set of all elements x of R such that f(x) = 0. Every ideal is the kernel of a ring homomorphism and vice versa.

Maximal ideal: A left ideal M of the ring R is a maximal left ideal if M ≠ R and the only left ideals containing M are R and M itself. Maximal right ideals are defined similarly. In commutative rings, there is no difference, and one speaks simply of maximal ideals.

Nil ideal: An ideal is nil if it consists only of nilpotent elements.

Nilpotent ideal: An ideal I is nilpotent if its powers I^k are {0} for k large enough. Every nilpotent ideal is nil, but the converse is not true in general.

Nilradical: The set of all nilpotent elements in a commutative ring forms an ideal, the nilradical of the ring. The nilradical is equal to the intersection of all the ring's prime ideals. It is contained in, but in general not equal to, the ring's Jacobson Radical.

Prime ideal: An ideal P in a commutative ring R is prime if P ≠ R and if for all a and b in R with ab in P, we have a in P or b in P. Every maximal ideal in a commutative ring is prime. There is also a definition of prime ideal for noncommutative rings.

Principal ideal: A principal left ideal in a ring R is a left ideal of the form Ra for some element a of R. A principal right ideal is a right ideal of the form aR for some element a of R. A principal ideal is a two-sided ideal of the form RaR for some element a of R.

Radical of an ideal: The radical of an ideal I in a commutative ring consists of all those ring elements a power of which lies in I. It is equal to the intersection of all prime ideals containing I.

Ring homomorphism: A function f : R → S between rings (R,+,*) and (S,⊕,×) is a ring homomorphism if it satisfies

f(a + b) = f(a) ⊕ f(b)

f(a * b) = f(a) × f(b)

f(1) = 1

for all elements a and b of R.

Ring monomorphism: A ring homomorphism that is injective is a ring monomorphism.

Ring isomorphism: A ring homomorphism that is bijective is a ring isomorphism. The inverse of a ring isomorphism is also a ring isomorphism. Two rings are isomorphic if there exists a ring isomorphism between them. Isomorphic rings can be thought as essentially the same, only with different labels on the individual elements.

Types of rings

Artinian ring: A ring satisfying the descending chain condition for left ideals is left artinian; if it satisfies the descending chain condition for right ideals, it is right artinian; if it is both left and right artinian, it is called artinian. Artinian rings are noetherian.

Boolean ring: A ring in which every element is idempotent is a boolean ring.

Commutative ring: A ring R is commutative if the multiplication is commutative, i.e. rs=sr for all r,s∈R.

Dedekind domain: A Dedekind domain is an integral domain in which every ideal has a unique factorization into prime ideals.

Division ring or skew field: A ring in which every nonzero element is a unit and 1≠0 is a division ring.

Domain (ring theory): A domain is a ring without zero divisors and in which 1≠0. This is the noncommutative generalization of integral domain.

Euclidean domain: A Euclidean domain is an integral domain in which a degree function is defined so that "division with remainder" can be carried out. It is so named because the Euclidean algorithm is a well-defined algorithm in these rings. All Euclidean domains are principal ideal domains.

Field: A field is a commutative division ring. Every finite division ring is a field, as is every finite integral domain. Field theory is in fact an older branch of mathematics than ring theory.

Finitely presented algebra: If R is a commutative ring and A is an R-algebra, then A is a finitely presented R-algebra if it is a quotient of a polynomial ring over R in finitely many variables by a finitely generated ideal.^[1]

Integral domain or entire ring: A commutative ring without zero divisors and in which 1≠0 is an integral domain.

Invariant basis number: A ring R has invariant basis number if R^m isomorphic to Rⁿ as R-modules implies m=n.

Local ring: A ring with a unique maximal left ideal is a local ring. These rings also have a unique maximal right ideal, and the left and the right unique maximal ideals coincide. Any ring can be made local via localization.

Noetherian ring: A ring satisfying the ascending chain condition for left ideals is left noetherian; a ring satisfying the ascending chain condition for right ideals is right noetherian; a ring that is both left and right noetherian is noetherian. A ring is left noetherian if and only if all its left ideals are finitely generated; analogously for right noetherian rings.

Prime ring: A non-trivial ring R is called a prime ring if for any two elements a and b of R with aRb = 0, we have either a = 0 or b = 0. This is equivalent to saying that the zero ideal is a prime ideal. Every simple ring and every domain is a prime ring.

Primitive ring: A left primitive ring is a ring that has a faithful simple left R-module. Every simple ring is primitive. Primitive rings are prime.

Principal ideal domain: An integral domain in which every ideal is principal is a principal ideal domain. All principal ideal domains are unique factorization domains.

Semisimple ring: A semisimple ring is a ring R that has a "nice" decomposition, in the sense that R is a semisimple left R-module. Every semisimple ring is also Noetherian, and has no nilpotent ideals. Any ring can be made semi-simple if it is divided by its Jacobson radical.

Simple ring: A non-zero ring with no non-zero two-sided ideals is a simple ring.

Trivial ring or zero ring: The ring consisting only of a single element 0=1. Zero ring also has another meaning, see below.

Unique factorization domain or factorial ring: An integral domain R in which every non-zero non-unit element can be written as a product of prime elements of R. This essentially means that every non-zero non-unit can be written uniquely as a product of irreducible elements.

Zero ring or null ring: A rng (ring without 1) in which the product of any two elements is 0 (the additive neutral element). Also, the zero ring, the ring consisting only of a single element 0=1 (see trivial ring, above).

Ring constructions

Direct product of a family of rings: This is a way to construct a new ring from given rings by taking the cartesian product of the given rings and defining the algebraic operations component-wise.

Endomorphism ring: A ring formed by the endomorphisms of an algebraic structure. Usually its multiplication is taken to be function composition, while its addition is pointwise addition of the images.

Localization of a ring: A technique to turn a given set of elements of a ring into units. It is named Localization because it can be used to make any given ring into a local ring. To localize a ring R, take a multiplicatively closed subset S containing no zero divisors, and formally define their multiplicative inverses, which shall be added into R.

Opposite ring: Given a ring R, its opposite ring 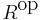$R^{\textrm{op}}$ has the same underlying set as R, the addition operation is defined as in R, but the product of s and r in 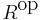$R^{\textrm{op}}$ is rs, while the product is sr in R.

Polynomial rings

Main article: Polynomial ring

Differential polynomial ring

Formal power series ring

Laurent polynomial ring

Monoid ring

Polynomial ring

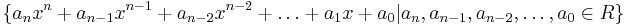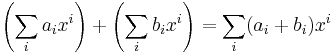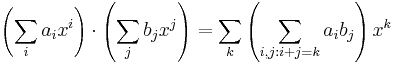Given R a commutative ring. The polynomial ring R[x] is defined to be the set $\{ a_n x^n %2B a_{n-1} x^{n-1} %2B a_{n-2} x^{n-2} %2B \ldots %2B a_1 x %2B a_0 | a_n , a_{n-1}, a_{n-2}, \ldots , a_0 \in R \}$ with addition defined by $\left(\sum_i a_i x^i\right) %2B \left(\sum_i b_i x^i\right) = \sum_i (a_i%2Bb_i)x^i$ , and with multiplication defined by $\left(\sum_i a_i x^i\right) \cdot \left(\sum_j b_j x^j\right) = \sum_k \left(\sum_{i,j: i %2B j = k} a_i b_j\right)x ^k$ .

Some results about properties of R and R[x]:

If R is UFD, so is R[x].
If R is Noetherian, so is R[x].

Ring of rational functions

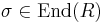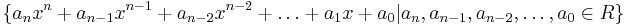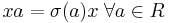Skew polynomial ring: Given R a ring and an endomorphism $\sigma \in \textrm{End}(R)$ of R. The skew polynomial ring $R[x; \sigma]$ is defined to be the set $\{ a_n x^n %2B a_{n-1} x^{n-1} %2B a_{n-2} x^{n-2} %2B \ldots %2B a_1 x %2B a_0 | a_n , a_{n-1}, a_{n-2}, \ldots , a_0 \in R \}$ , with addition defined as usual, and multiplication defined by the relation $xa = \sigma(a) x \;\forall a \in R$ .

Miscellaneous

Characteristic: The characteristic of a ring is the smallest positive integer n satisfying nx=0 for all elements x of the ring, if such an n exists. Otherwise, the characteristic is 0.

Krull dimension of a commutative ring: The maximal length of a strictly increasing chain of prime ideals in the ring.

Ringlike structures

The following structures include generalizations and other algebraic objects similar to rings.

Nearring: A structure that is a group under addition, a semigroup under multiplication, and whose multiplication distributes on the right over addition.

Rng: An algebraic structure satisfying the same properties as a ring, except that multiplication need not have an identity element. The term "rng" is meant to suggest that it is a "ring" without an "identity".

Semiring: An algebraic structure satisfying the same properties as a ring, except that addition need only be an abelian monoid operation, rather than an abelian group operation. That is, elements in a semiring need not have additive inverses.

Notes

^ Grothendieck & Dieudonné 1964, §1.4.1

References

Grothendieck, Alexandre; Dieudonné, Jean (1964). "Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné) : IV. Étude locale des schémas et des morphismes de schémas, Première partie". Publications Mathématiques de l'IHÉS 20. MR 0173675. http://www.numdam.org:80/numdam-bin/feuilleter?id=PMIHES_1964__20_.